T2. FUNCIONES RECURSIVAS: PROBANDO, PROBANDO...

HONGOS Y HOJARASCA EN EL SOTOBOSQUE DE LA LAURISILVA DE LOS MONTES DE LOS REALEJOS, NOROESTE DE TENERIFE.

     Imaginémonos la siguiente situación: tomamos nuestro smartphone, lo encendemos y, al cabo de unos segundos, se nos pide en pantalla que introduzcamos nuestro número pin para dejarlo operativo. Sobre el teclado y el campo de introducción de clave se nos muestra, destacado, un mensaje de lo más inquietante: "Dispone usted de tres intentos". Da la casualidad de que la noche anterior estuvimos de celebración, vulgo farra o tenderete, y hoy nos hemos levantado un tanto embotados de los sentidos. Tecleamos los cuatro o cinco numeritos de marras... y nos sale el mensajito de error. ¡Mecachis! "Dispone usted de dos intentos", leemos con resacado estupor en la parte superior de la pantalla. Un par de segundos más tarde, tras rascarnos la desordenada pelambre, sonreímos, condescendientes con nosotros mismos. "Ya sé - pensamos -. El uno iba antes del dos, claro, y por eso metí la pata". Tecleamos nuestro pin de nuevo convencidos y ufanos de nuestra memoria y capacidades deductivas (¡bueno estaría!)...

"Error. Dispone usted de un intento". No nos lo podemos creer. Nos hemos vuelto a equivocar. O eso dice el maldito aparato de Satanás. ¿Por qué? ¿En qué? De la euforia postetílica pasamos al pánico en cuestión de nanosegundos. Se nos viene al caletre que existía un número, un tal puck o algo así, que venía en las instrucciones, o en la cajita,  o en el contrato, o en vaya usted a saber, o en algún sitio de ésos y que servía para desbloquear el móvil. Un número que, como pasa con Santa Bárbara, sólo nos acordamos de él cuando truena. Y ahora mismo está a punto de caernos un tormentón de los gordos. ¿Quién diantre se acuerda del número ése con nombre de duende? ¿Quién es el guapo/a que se lo aprende de memoria? ¡Venga ya, hombre!

Sudor frío, temblor de manos, pupilas dilatadas. Solo se escucha el tic tac del reloj del salón, a kilómetros de distancia. La mañana se ha vuelto gris y los pájaros, en el parque, han enmudecido su cantar.

Tras un largo minuto de indecisión y producto de un colosal esfuerzo de memoria abriéndonos paso en la espesura de una buena noche, llegamos a una conclusión: "¿Sería así? A lo mejor era así... El tres que venía después del uno, el ocho entre el dos y el tres, ... No podemos seguir así. Tomamos una decisión valiente, arriesgada, temeraria. Pedimos auxilio a la divinidad en nuestro fuero interno... y tecleamos el número con húmeda parsimonia. Nos sentimos al cabo de un juicio, cuando nos piden que nos pongamos en pie para escuchar la sentencia del juez.

Tomamos aliento antes de pulsar la tecla de "aceptar" que, de repente, se nos ha trasmutado en boca del infierno.

Cerramos los ojos, los apretamos con fuerza. Notamos que se nos llena la vejiga. Las palpitaciones se multiplican, se nos sube la tensión, se nos baja el azúcar... Y apretamos la dichosa tecla.

La ruedecilla gira. Transcurre un segundo. La ruedecilla gira. Pasa un segundo y medio. Somos presa de un ataque de ansiedad. "Nunca jamás en mi vida vuelvo a salir de noche. Palabra". La ruedecilla gira, y gira,...

¡Música! ¡La música! ¡Por fin ese repulsivo soniquete de m...da que ahora nos suena, mira tú por dónde, a música celestial! El pin es correcto.

La mañana del domingo vuelve a ser maravillosa.

¿Qué es lo que ha provocado todo esto en nosotros? Una función recursiva con su inseparable contador (de intentos).

La función recursiva, llamada recursiva o, simplemente, recursividad es aquella función definida por el usuario que es capaz de llamarse a sí misma a partir de una cierta condición, incluida en su propio bloque de código, en el cuerpo de la función.

Resultan particularmente útiles en determinados casos como el que hemos expuesto en el ejemplo, ingreso de claves o passwords, cálculos cerrados, etc. Python permite la creación de funciones recursivas capaces, como acabamos de decir, de llamarse a sí mismas de modo análogo a como invocaríamos a una función corriente.

Para el caso anterior, podríamos proponer la siguiente función recursiva:

Comenzamos en 1. declarando una función def a la que ponemos por nombre pin, y a la que pasamos un único argumento, un argumento opcional que se corresponde con una asignación, con la variable intento, a la que proporcionamos un valor inicial y por defecto de tipo numérico, un entero de valor 1.
Ya en 2. creamos el input, la entrada de datos por parte del usuario siguiendo la sintaxis habitual, declarando una variable, resp, a la que asignaremos como valor la respuesta proporcionada por el usuario.
En la siguiente línea de código, en 3., introducimos ya el condicional if donde la condición a valorar por el intérprete de Python será si la respuesta proporcionada por el usuario y que hemos almacenado en la variable resp, es distinta (operador de comparación !=) a la que hemos propuesto nosotros. Fijémonos que hemos pasado las cuatro cifras de nuestro código pin <<correcto>> en modo string, esto es, entrecomillado, a la manera de una cadena de texto o de caracteres literales, dado que, como ya sabemos, toda introducción de datos (input data) asume el tipo de dato string por defecto. de esta forma, caracterizando nuestro pin como "1234" como una cadena de caracteres, evitamos conflictos y código innecesario de tipado. Hasta aquí nada nuevo.
Ahora, en 4., colocamos un segundo condicional if, convenientemente indentado con respecto al condicional anterior (hablamos, pues, de un condicional anidado), del que es subsidiario. En este caso, la condición que establecemos es que el valor de la variable intento sea menor que 3. ¿Por qué 3? porque hemos decidido que el usuario disponga de un número máximo de tres intentos. Si hubiéramos decidido que, por ejemplo, dispusiera de cinco oportunidades, tendríamos que haber puesto el entero 5 a la derecha del operador de comparación.

PATIO TÍPICO CANARIO

A partir de ahora nos encontramos con el bloque de código (el correspondiente al del segundo if), donde le decimos al intérprete de Python lo que tiene que hacer. Lo primero de todo, en 5., es proporcionar un texto en pantalla mediante el recurso a la función print() en el que se nos advierte de que hemos cometido un error, e instándonos a que introduzcamos de nuevo el dichoso número pin.
En 6. tenemos una de las claves del script. Aquí introducimos el 'contacto'. Mediante el operador aritmético += sumamos una cantidad, en este caso, 2, a la variable intento aumentando su valor de 1, al comienzo pues, recordemos, éste era su valor inicial en la zona de argumentos de la función, a 3 (1 + 2).
Justo debajo, a continuación, tal y como señalamos a través del comentario adjunto a la línea de código, implementamos una llamada recursiva. Nuestra primera llamada recursiva, que nos devuelve a la línea uno del script de forma que el intérprete de Python inicie de nuevo el proceso (y de aquí el concepto de recursividad) mediante la llamada o invocación recurrente a la función pin.
Instauramos en 7. un tercer condicional if, (segundo nivel de anidación) debajo de la llamada recursiva (o retrollamada, como se la conoce también en algunas partes) a la función cuya condición es exactamente la misma que propusimos en la línea 4. del código: que intento sea menor que 3.
A renglón seguido, en 8., volvemos a echar mano del contador y repetimos el código que escribimos en 6., esto es, incrementar en 2 mediante el operador += en l valor de la variable intento.
Inmediatamente después, segunda llamada recursiva mediante la instrucción pin(intento) que ya empleamos en la llamada precedente.

Una vez efectuada la llamada, insertamos una cláusula else correspondiente a nuestro tercer if (¡cuidado con las indentaciones! 🔔). Dicha cláusula contendrá dos líneas de código: la primera, 9., se corresponde con un texto que se mostrará al usuario mediante la función print() y en el que le advertimos de que le resta tan sólo un último intento. La segunda línea es nuestra tercera y última llamada recursiva: pin(intento).
Colocamos una segunda cláusula else para cerrar convenientemente nuestro segundo condicional if, 10., y le ponemos como contenido único, la palabra reservada pass. La sentencia pass constituye un tipo específico de sentencia que le indica al intérprete de Python que no es necesario efectuar acción alguna; en resumidas cuentas, 'que no haga nada'. La sentencia pass se utiliza habitualmente cuando no queremos que se haga nada en una sentencia que requiere a su vez de de otra, como por ejemplo:

                                                                                    >>> while True: Pass *

* Esto es, lo que se llama, un bucle infinito. mientras (while) lo que quiera que se esté ejecutando (el análisis) arroje como resultado de la evaluación de la condición True, no se haga o ejecute nada.

      A TÍTULO INFORMATIVO, LA SENTENCIA PASS ES MUY SOCORRIDA CUANDO UN PROGRAMADOR ESTÁ DESARROLLANDO LA ESTRUCTURA BÁSICA DE UN PROGRAMA ANTES DE 'RELLENARLO', PUESTO QUE AÚN NO CONOCE LAS INSTRUCCIONES QUE LE DARÁN SU FORMA FINAL, Y LE CONVIENE MANTENER FUNCIONAL LA ESTRUCTURA PARA HACER TESTEOS. UNA VEZ COMPROBADO QUE LO CODIFICADO HASTA AHORA RESPONDE A SUS EXPECTATIVAS  GRACIAS A QUE LA SENTENCIA PASS LE HA PERMITIDO RECORRER SU ESTRUCTURA SIN NECESIDAD DE INSERTAR TANTO CÓDIGO. MÁS ADELANTE, SUSTITUIRÁ LA SENTENCIA POR LOS TROZOS DE CÓDIGO QUE ESTIME OPORTUNOS.

Colocamos en 11. la última cláusula else para el primero de nuestros condicionales if, y en 12. colocamos el texto que deberá imprimirse en pantalla: "NÚMERO DE PIN CORRECTO".

VISTA DEL VALLE DE AGUERE. TENERIFE.

Aquí mostramos otro ejemplo de de función recursiva más sencillo (y más zen, 👍):

Vamos a estudiar un último ejemplo de recursividad y, con él, dar por concluida esta entrada. Lo haremos de la mano de los profesores Andrés Marral e Isabel Gracia, en su libro Introducción a Python, Universitat Jaume I, apoyándose en una variante más científica: el cálculo recursivo de un factorial.
De nuevo,...¡Que no cunda el pánico! Veremos que resulta más fácil y asequible de lo que pudiéramos pensar.
Primero vamos a ver su formulación matemática:

✽ Donde cualquier número factorial N se representa así: N!, de tal modo que el factorial de 5, por ejemplo, se representa como 5!.
Digamos antes de proseguir que una FACTORIZACIÓN constituye una técnica matemática que nos permite hallar dos o más factores (divisores), cuyo producto sería igual a la expresión matemática que proponemos, un número entero, de acuerdo al máximo común divisor del mismo.
Toca ahora "traducir" la fórmula matemática que acabamos de mostrar a un bloque de código, un script, comprensible para el intérprete de Python. Quedaría algo así:

Donde n es el número entero que queremos factorizar. ¿Dónde está la recursividad? Imaginemos que pasamos el número 5 como argumento de la función factorial. Una vez comprobado que el valor de n no es ni 1 ni 0, en cuyo caso nos devolvería automáticamente el valor 1, el intérprete de Python comienza a calcular el factorial de 5. Pero, claro, cuando llega a la li´nea 5 del código... ¡Ostras! ¿Qué pasa aquí? Que le toca llamar el factorial de n-1, esto es, 5 - 4, luego el factorial de 4 para poder completar la expresión que hemos propuesto (n * factorial(n- 1)). Así que, "vuelta pa'rriba"y a calcular ahora el factorial de 4. El intérprete de Python comprueba que, en efecto, n - 1 no es 0 ni 1, y continúa leyendo el bloque de código. Comprueba en la cuarta línea de código que 4 es mayor que 1, pasa a la quinta... y de nuevo, topetazo: n - 1. Como ahora n era igual a 4, al restarle 1 se nos queda en 3, el nuevo valor que toma n ahora, y vuelta a empezar. Y así sucesivamente hasta que n=1. En este caso, por mor de la segunda y tercera línea del bloque de código, ya puede cerrar ese bucle, llegar a la línea sexta y devolver el resultado pues el intérprete de Python ya lo conoce. Ahora ya puede pasar al número siguiente, 2: ahora que ya sabe que el factorial de 1 es 1, pasa a la quinta línea y ejecuta el algoritmo, n * factorial(n - 1), esto es, 2 (que es el valor que tiene n en ese momento, ¡ojo!) * factorial(2 - 1), que deviene en, 2 * factorial(1). Y como el factorial de 1 es 1, , se nos queda en 2 * 1, que es igual a 2. El 2 será el siguiente número devuelto.

Ahora, el intérprete de Python, sabe que el factorial de 2 es 2, lo multiplicará por 3, que es el siguiente valor que adopta n, en virtud de la expresión que muestra la quinta línea de código, tal cual hemos visto con anterioridad. En consecuencia, devuelve el valor 6.
Ya tenemos que el valor de factorial 3 es 6. Lo multiplicará por 4, que es el valor de n que "toca" ahora, y nos devolverá 24 al ejecutar la sexta línea de script.
Y, por fin, llegamos ya al valor original de n, 5. Pues nada: el mismo procedimiento que se ha llevado con todos los enteros anteriores hasta el 1 (4, 3, 2, 1) y a consignar el resultado. En este caso, será 24 lo que multiplicará por 5. El valor de esta multiplicación es 120. Esta es la respuesta a factorial(5).
Veamos:

Con la inclusión de una simple función print() podemos visualizar impresa en pantalla la secuencia completa de factoriales parciales:

Mostramos a continuación un "árbol de llamadas" para clarificar aún más el proceso:

Podemos, sin embargo, resolver el cálculo de 5! factorial apoyándonos en un simple bucle for/in, esto es, sobre un iterador:

Con esto queremos decir que a toda función recursiva es posible "oponer" al menos, otra función iterativa que, al menos, independientemente de su legibilidad (recordemos, la claridad del código) y/o elegancia, suele mostrarse más eficiente que en sus versiones recursivas ahorrando en tiempo y uso de memoria.
Y ya que hemos tomado carrerilla, la propina final, apoyándonos en el texto y los autores que hemos mencionado con anterioridad. Nos proponen calcular el máximo común divisor (mcd) de los números 'n' y 'm' recurriendo para ello en el Algoritmo de Euclides.

     SEGÚN LO HE ESTUDIADO YO EN LA ACADÉMICA PERRUNA, EL ALGORITMO DE EUCLIDES VIENE A DECIR LO SIGUIENTE: "CALCULA EL RESTO DE DIVIDIR EL MAYOR DE LOS DOS NÚMEROS POR EL MENOR DE ELLOS. SI EL RESTO ES 0, ENTONCES EL MÁXIMO COMÚN DIVISOR (MCD) ES EL MENOR DE AMBOS NÚMEROS. SI EL RESTO ES DISTINTO DE 0, EL MÁXIMO COMÚN DIVISOR (MCD) DE n Y m ES EL MÁXIMO COMÚN DIVISOR DE OTRO PAR DE NÚMEROS: EL FORMADO POR EL MENOR DE n Y m Y POR DICHO RESTO". 




Los autores nos invitan a continuación a enfrentar el problema primero "a lápiz", con los dos números dados n=500 y m=218, y después, tratar su traducción al código de Python. Vamos allá:

• Empezamos calculando el resto (%) de dividir 500 entre 218, el mayor entre el menor.El resto deviene en 64. Como el resto no es 0, aún no hemos terminado, tenemos que calcular el máximo común divisor de 218, el menor entre ambos números, y 64, el resto que acabamos de obtener.
• Empezamos dividiendo 500 entre 218. Ahora toca dividir 218 entre 64. El resto de esta nueva división es 26, que no es 0, evidentemente. En consecuencia, debemos seguir calculando el máximo común divisor. Esta vez será entre 64 y el nuevo resto devuelto: 26.
• El resto de dividir 64 entre 26 es 12, que tampoco, ¡vaya por Dios!, es 0. Pues nada: tenemos que seguir calculando el máximo común divisor entre 26 y 12.
• Procedemos, y el resto de dividir ahora 26 entre 12 es 2. Tampoco es 0... y la punta del lápiz está ya casi gastada. Bueno, seguimos a ver: toca ahora dividir 12 entre 2.
• El resto de dividir 12 entre 2 es... ¡0! ¡Por fin!¡Ya hemos llegado a 0! Ahora podemos asegurar henchidos de orgullo y gloria que el máximo común divisor de 500 y 218 es 2.

LAURISILVA  ABIERTA EN LOS MONTES DE GÜÍMAR, CENTRO SUR DE TENERIFE.

Con el ejemplo que acabamos de estudiar se hace explícitamente que una y otra vez resolvemos el mismo problema (he aquí la esencia misma de la recursividad: ejecutar una y otra vez un mismo algoritmo en factores diferentes hasta cumplir una determinada condición que provoca la deseada bifurcación), sólo que con datos diferentes. Si analizamos el algoritmo en términos de recursión encontramos que el caso base es aquél en el que el resto (%) de la división en 0 y, el caso general, cualquier otro.
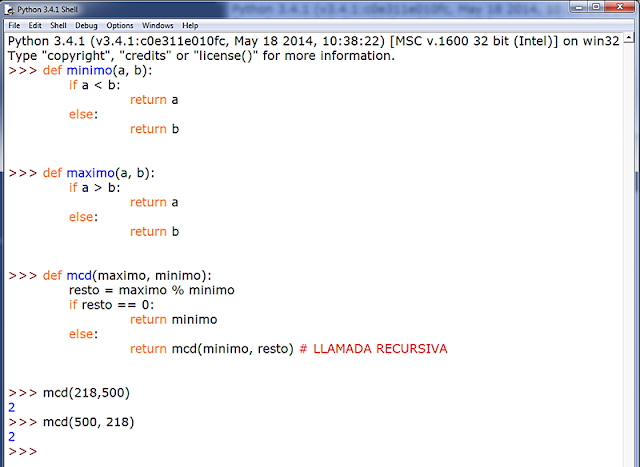
Para construir el programa debemos saber primero cuál es el número mayor (máximo) y cuál es el menor (mínimo), por lo que nos vendrá bien definir antes funciones que efectúen ese cálculo:

Y completamos el programa con la función que calcula el Algoritmo de Euclides:

Como ya hemos aprendido, toda función recursiva puede ser traducida (y viceversa) a una iteración.

DIQUE Y CRESTA COMO CONSECUENCIA DE LA EROSIÓN SOBRE UNA EXTRUSIÓN VOLCÁNICA, SEPARANDO BARRANCOS EN LAS CUMBRES DE TAGANANA,  MACIZO DE ANAGA,  NORESTE DE TENERIFE.