T4. CLOSURES: LA SONRISA DE LAS MATRIUSKAS

BARRANCO DE IFONCHE, ENTRE ARONA Y VILAFLOR, CON LOS PRIMEROS MANCHONES DE PINAR EN DIRECCIÓN A LA CUMBRE,. SUROESTE DE TENERIFE.

      El concepto de closure, 'cierre', en inglés, atañe a las funciones anidadas, una forma de crear un árbol de funciones dependientes unas de otras como puede serlo un árbol de carpetas y subcarpetas en nuestro disco duro. Ya hemos visto alguna cosa en las páginas dedicadas a las funciones definidas por el usuario y nuestra pretensión ahora es profundizar lo necesario para comprender mejor este particular recurso de programación.

Entrando al tajo, tenemos que atenernos a un requisito previo fundamental: para que el asunto funcione, hay que respetar religiosamente los espacios de nombre, los namespaces, con los que definimos (y volvemos callable) una función cualquiera `para poder llamarla/invocarla más adelante en nuestro código cuando nos fuera necesario, en tanto que una variable cualquiera que hayamos declarado con un nombre x, el que sea, en la función matriz o principal, puede ser accedida desde el código de una función anidada (hija o secundaria).
Más técnicamente, podemos incluir la definición que nos ofrece d. Arturo Fernández Montoro en Python 3 al descubierto, de la editorial rclibros, y que viene a decir lo siguiente: un closure o una Factory Function como también se la llama, es un técnica de programación que permite a una función acceder a variables que, a priori, están fuera de su ámbito (scope) de acceso.

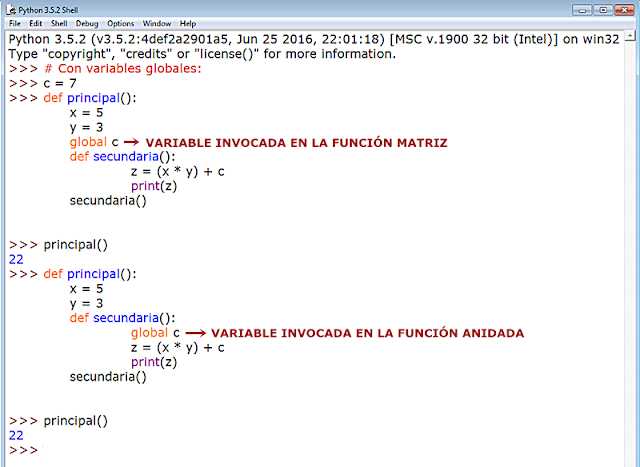
Veamos una muestra para abrir boca:

En el ejemplo superior tenemos una función matriz que llamamos principal, en cuyo cuerpo serrano declaramos dos variables locales con sus respectivas asignaciones: x = 5 e y = 3. A continuación, definimos una segunda función y, en consecuencia, anidada a la función principal, que llamamos secundaria, respetando así el espacio de nombres para que no se generen incompatibilidades en futuros usos de las variables respectivas. En el cuerpo de esta segunda declaramos una variable z que almacenará el resultado de la ejecución de la expresión x * y que, finalmente, nos imprimirá en pantalla con print(z). Observemos que las variables x e y declaradas en la función matriz las llamamos en el cuerpo de la una función diferente, aunque dependiente de la primera por estar anidada a ella, y es aquí, con z, donde hacemos uso de sus valores para obtener un resultado.

Esto es lo que queremos decir cuando decimos que las variables de la función matriz son accesibles para la/s función/es secundaria/s.

Sin embargo, como ya sabemos que las funciones definidas por el usuario deben llevar un nombre para ser invocadas (para que puedan  ser callable) y sólo cuando se las invoca es cuando despliegan su funcionalidad, para que la función secundaria actúe y ejecute la expresión debemos llamarla. ¿Y desde dónde la llamamos? pues por pura lógica desde el pie de su función matriz con la sintaxis de llamada habitual: secundaria(). Este procedimiento es lo que se conoce como autollamada, de modo análogo a como se ejecutan las funciones recursivas. Si no efectuáramos la llamada, el intérprete de Python nos lanzaría una excepción.

Nótese que no hemos usado ninguna cláusula return ni print() al pie de la función principal, pues éste ya viene implícito con la llamada a secundaria() que ya contiene un print(z).

Del mismo modo no debemos llamar directamente a la función secundaria porque ésta es un elemento más del cuerpo de la función principal y, como tal, no es accesible desde fuera de la función principal, lo que generaría una excepción del tipo de NameError.

En los dos ejemplos que siguen podemos comprobar que no existe problema alguno para incorporar variables globales a nuestro código, resolviéndose en ambos casos con un resultado satisfactorio independientemente de que se las invoque en la función matriz o en la anidada.

Llegados hasta aquí podemos definir más técnicamente un closure como una combinación de ámbito, alcance, competencia (scope) y código (code), del website www.bogotobogo.com, de K. Hong (Doctor en Filosofía. / Golden Gate Ave., San Francisco / Universidad Nacional de Seúl / Carnegie Mellon / UC Berkeley / DevOps / Aprendizaje Profundo / Visualización).

PARADOR NACIONAL DE LAS CAÑADAS DEL TEIDE DESDE LOS ALTOS DE GUAJARA. PARQUE NACIONAL DE LAS CAÑADAS DEL TEIDE, CENTRO DE TENERIFE.

Siguiendo con la síntesis de K. Hong, una función def combina una porción de código que debe ser ejecutada y el ámbito concreto en que se ejecuta. Sin embargo, la mayoría de las veces en que se habla de closures, nos referimos a una función anidada y al ámbito de la misma. A veces queremos una función que retenga, conserve (to retain) un determinado valor cuando ésta fue creada incluso aunque el ámbito dejara de existir.

A esta técnica de Python que nos permite usar valores propios de parámetros externos dentro de una función dinámica, es otra forma de entender los closures:

Vamos a estudiar un ejemplo:

En 1. declaramos la función principal, matriz o envolvente en un closure. En este caso lleva dos parámetros: a y b.

En 2. insertamos una expresión asociada a la variable c en el cuerpo de la función principal.

En 3. seguimos en el cuerpo de la función matriz y declaramos una nueva función (anidada) dentro del ámbito (scope) de la mencionada función principal. Fijémonos que no lleva parámetros, al menos, en principio porque no disponemos de acceso directo a la función secundaria por lo que tampoco podemos pasarle parámetros: podemos llamar o invocar a la función matriz, principal o envolvente (es callable) pero no podemos hacerlo sobre la secundaria o anidada porque se incrusta en el ámbito local de una función y, en consecuencia,  no es accesible desde fuera de la función matriz, principal o envolvente (no es callable). Resumiendo, a la función anidada sólo la puede llamar su función matriz y nunca nosotros. La función secundaria "hereda" lo ejecutado previamente en la función principal, matriz o envolvente y lo incorpora a su propio ámbito.

En 4. incorporamos el resultado de la ejecución de la expresión en el ámbito de la función principal llamando a la variable c, y creamos una nueva expresión, la potencia al cuadrado de c, que asignamos a la variable pot.

En 5. conseguimos la devolución del resultado de la ejecución de la expresión. ¡Cuidado! Si usáramos la cláusula return no obtendríamos resultado alguno porque no nos permite invocar a la propia función anidada para que ejecute su labor, por lo que debemos recurrir a la función print() pata visualizar el resultado en pantalla.

En 6. llamamos a la función potencia() para que ejecute su código (autollamada), eso sí, desde el ámbito de la función principal, matriz o envolvente.
En 7. tenemos el pie de la función principal, matriz o envolvente (si queremos incluirlo), que devolverá el resultado de la ejecución de la expresión c = a + b en el cuerpo de la función principal, matriz o envolvente después de devolver (lo hemos puesto encima de la cola de llamadas) el resultado de la ejecución de la función potencia().

      SOBRE ESTE EJEMPLO PODRÍAMOS HABER EJECUTADO LA LLAMADA A TRAVÉS DE LA SINTAXIS DE PUNTO, PERO A PESAR DE QUE NOS DEVUELVE EL RESULTADO ESPERADO, INMEDIATAMENTE DESPUÉS PYTHON NOS LANZA UNA EXCEPCIÓN DEL TIPO ERROR DE ATRIBUTO:

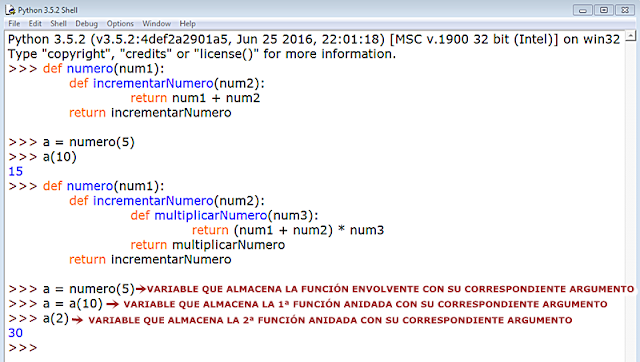
Veamos otro ejemplo:

Con este ejemplo mostramos cómo podemos pasar parámetros dentro de una función anidada, incluso, en una "cascada", como ocurre con el segundo ejemplo. Para poder obtener un resultado es necesario declarar primero una variable donde almacenar el resultado de la ejecución de la función a la que llamamos, en nuestro caso, la variable a, con su/s correspondiente/s paso de parámetros. 

Podemos establecer distintos niveles de anidamiento, tres en el ejemplo de la "cascada", con sus respectivas llamadas. Fijémonos en que luego, para conseguir resultados, debemos ir pasando parámetros en orden descendente: primero a = numero(5) que llama a numero, luego a = a(10) para la segunda función anidada que llama a incrementarNumero y, finalmente, a(2) para la última, que llama a multiplicarNumero. Nótese también que para ahorrarnos nombres de variables hemos ido reasignando las funciones a una misma variable a.

Señalemos también que la instrucción que devuelve el resultado final, return (num1 + num2) * num3 ⇒ 30, se sitúa en el ámbito (o scope, que también se llama así) de la última función anidada declarada.

Podemos obtener resultados parciales subdividiendo los procesos y mostrar resultados parciales con print().

Si en lugar de utilizar la misma variable a por el procedimiento de reasignación utilizáramos tres nombres de variables distintos, por ejemplo, a =numero(5); b = a(10) y c = b(2), comprobaríamos que las variables a, b y c conservan sus valores a la vez que son declaradas.

AL FONDO, ERAS ESCALONADAS PARA LA TRILLA DEL TRIGO CONSTRUIDAS APROVECHANDO LA COLADA DE LAVA. A LA DERECHA, MONTEVERDE DE ALTURA Y, EN PRIMER PLANO, CAMPO DE AMAPOLAS EN LA PRIMAVERA DE EL TANQUE, NORTE DE TENERIFE.

Cuando, por ejemplo, creamos a, la función principal, envolvente, de nivel superior o, también, de nivel 1 (escoja usted) numero(num1) utiliza a la función anidada incrementarNumero(num2) como valor de retorno, teniendo en cuenta que es la propia función la que se retorna y no el valor de retorno de la propia función.

La función interna no es llamada desde dentro de la función principal numero(num1). Así pues, numero(num1) es una función (principal) que retorna una función (anidada) cuando es llamada o invocada.

De este modo, nuestro programa puede contar con una referencia externa a la función anidada y, a su vez, la función anidada conserva su referencia en el objeto llamada, incrementarNumero(num2)  de la función externa.

Analicemos el siguiente ejemplo:

En 1. definimos una función típica y corriente que suma dos argumentos que introduciremos en la correspondiente zona de parámetros (paso de parámetros cuando la llamemos: suma(a, b).

En 2. definimos una segunda función, llamada(funcion), que llevará como argumento otra función. Esta función imprimirá en pantalla el resultado que arroje la ejecución de la función que le pasemos como argumento. Pero para que el código funcione, debemos pasar los parámetros que vaya a llevar la función que pasemos a su vez como argumento de suma(a, b), en el ejemplo, 7 y 9.

Finalmente, en 3. realizamos la llamada a la segunda función,llamada(funcion), y le pasamos como argumento el nombre de la primera función, suma(a, b), aunque eso sí, como ya dispone de los argumentos numéricos que se corresponden con a y b, es decir, 7 y 9, tan sólo tenemos que pasar su nombre: llamada(suma).

Pues bien, el desarrollo anterior puede ser convertido a closure del siguiente modo:

En 4. ahora la función llamada(funcion) no lleva argumento alguno pues "hereda" (inherit) los argumentos de su función envolvente. Será aquí, en el propio ámbito (scope) de nuestra función anidada llamada(funcion) donde se va a ejecutar el código.

En 5., como sucede con toda función, para que ejecute su trabajo, debe ser llamada/invocada, cosa que hacemos tras cerrar la función anidada con su pie, print(a + b), dentro del ámbito de la función envolvente o principal suma(a, b).

Nos despedimos con un último ejemplo. En esta ocasión, nos apoyamos en un condicional if/else para decidir si se llama a una función anidada u otra distinta en función de un dato obtenido previamente en el flujo de ejecución de la función envolvente o principal numeros(). Además, la entrada de datos no se pasa como argumento (la función no lleva parámetros) sino a través de un input().

Los closures pueden resultarnos particularmente útiles cuando nos conviene aglutinar una serie de acciones o funcionalidades (funciones) posibles como respuesta al resultado concreto de la ejecución de una única función principal o envolvente en pleno runtime (tiempo de ejecución). Este último ejemplo que acabamos de proponer nos proporciona una idea aproximada de lo que queremos explicar.

PINAR EN LOS ALTOS DE IGONCE, EN LA PARTE ALTA DEL MUNICIPIO DE CANDELARIA, RENACIDOS SOBRE VIEJAS TERRAZAS DE CULTIVO (VER LOS MURETES) ABANDONADOS, SURESTE DE TENERIFE.

Un lector de este blog, Csr_Varela, ha efectuado una consulta con el texto siguiente:

¿Cómo puedo comparar el resultado de dos funciones? Por ejemplo, estoy utilizando el API de un broker, y dentro de las funciones le solicito que me promedie el valor de cierre de los últimos 21 días de x valor y otras función que me promedie el cierre de los últimos 13 días de x valor? ¿Cómo hago para comparar esas funciones? Es decir, comparar el resultado de los números que me dan. Porque intento llamarlos inclusive desde global...

Bien, podemos ofrecer la siguiente solución a través de un closure:

En este ejemplo contamos con dos listas de datos: una lista con 21 valores (lista21)  y otra lista con 13 valores distintos (lista13) todos ellos en un tipo de datos float. Si quisiéramos que la lista13 contuviera los últimos trece datos de lista 21, nos basta con un slice: lista13 = lista21[9:22].
La relación entre dos o más funciones se da en una marco común que acoja a estas funciones para poder relacionarlas entre sí: Con closure podemos crear una función PRINCIPAL que acoja en su ámbito a estas dos funciones que señalas como funciones SECUNDARIAS.
Así, nuestra función PRINCIPAL  que acogerá en su ámbito a estas dos funciones promediadoras que citas, la llamaremos funcion_closure, como vemos en 1., y que llevará en su zona de parámetros ambas listas, lista21 y lista13.
Tras la cabecera de la función principal declaramos sendas variables, vprom21 y vprom13, que tendrán como cometido almacenar el resultado de la ejecución de las funciones SECUNDARIAS para poderlas manejar a posteriori desde la función PRINCIPAL funcion_closure. Como debemos inicializarlas para que Python las reconozca como variables, les proporcionamos a ambas el valor 0.
A continuación, introducimos, indentadas, las dos funciones SECUNDARIAS que necesitamos para promediar cada lista: funcion_21, en 2. y funcion_13, en 5., y recuperamos asímismo las variables vprom21 y vprom13 de nuestra función PRINCIPAL, ya que los closures permiten "trasladar, compartir, prestar" de manera fácil y sencilla sus propias variables como variables dentro del ámbito de sus funciones hijas o secundarias, por lo que no tenemos necesidad de recurrir a la palabra reservada global para llamarlas. A cada una de estas variables, como vemos en 3. y 6. les asignamos un algoritmo que permite calcular y redondear el resultado de la media aritmética (o cualquier otro cálculo que queramos implementar).
La clave está en las líneas 4. y 7., que, si te fijas, están fuera del ámbito de las funciones SECUNDARIAS y se sitúa, por contra, dentro del ámbito de la función PRINCIPAL. y a la que asignamos la ejecución de cada una de las funciones SECUNDARIAS, es decir, sobre vprom21 llamamos a la función SECUNDARIA funcion_21, ésta se ejecutará, y el resultado devuelto se almacenará en ella; y sobre vprom13 llamamos a la función SECUNDARIA funcion_13, ésta se ejecutará, y el resultado devuelto se almacenará en ella.
Con esto, ya tenemos dentro de la función PRINCIPAL funcion_closure los valores promedio que se corresponde con la ejecución de las dos funciones SECUNDARIAS funcion_21 y funcion_13, y con el código que hemos añadido a su cuerpo en 8. y 9., podemos manejar ambos resultados a nuestro antojo: en 8. imprimiéndolos en pantalla, y en 9. comparándolos, todo ello, dentro de una misma y única función.
Si quieres intentarlo con un Clase en lugar de con un closure, tienes toda la información que necesitas en los capítulos que siguen a INTRODUCCIÓN A LA PROGRAMACIÓN ORIENTADA A OBJETOS.